|
Home » Materiale didattico » Dispense e articoli » Effetto fotoelettrico |
|
Effetto fotoelettrico Introduzione. Verso la seconda metà del XIX secolo c’era la convinzione che la meccanica "classica" (Newton e sviluppi successivi), l’elettromagnetismo (sostanzialmente riassunto dalle equazioni di Maxwell) e la termodinamica (Carnot, Joule e altri) dovessero permettere di inquadrare tutti i fenomeni naturali anche quelli ancora di difficile interpretazione. Tuttavia negli ultimi anni del secolo, e nei primi di quello successivo, vennero fatte nuove scoperte che in alcun modo potevano essere inquadrate nei modelli precedenti. Questi fenomeni riguardavano il mondo dell’ infinitamente piccolo. Fenomeni connessi con la struttura intima della materia e su come le parti più piccole della materia interagiscano e scambino energia tra di loro. La stessa esistenza e stabilità degli atomi non era spiegabile nei termini della fisica classica. Queste scoperte portarono allo sviluppo di una "nuova" fisica che cambiò in maniera radicale il modo di descrivere i fenomeni naturali. I fisici dovettero "inventare" non solo nuovi concetti ma anche un opportuno formalismo matematico che permettesse di schematizzare la realtà fisica. Del resto anche Newton dovette inventare il calcolo differenziale per poter sviluppare compiutamente le sue teorie. E’ anche a causa di questo complesso formalismo matematico che la Meccanica Quantistica (la "nuova" fisica) risulta di difficile comprensione per i non "addetti ai lavori". La "potenza" dei metodi della meccanica quantistica sta non solo nel riuscire ad inquadrare in modo organico praticamente tutte le conoscenze attuali e nell’essere riuscita a prevedere numerosi fenomeni, poi puntualmente osservati, ma anche nell’aver inquadrato, come caso limite, le varie teorie della "fisica classica". In un primo momento i fisici cercarono dei modelli "ad hoc" per le varie classi di fenomeni. Non si trattava di un ritorno all’aristotelismo, ma di un tentativo di descrivere in un modo completamente nuovo ciò che si osservava sperimentalmente. Tutti questi modelli sviluppati "ad hoc", avevano però un punto fondamentale in comune: l’energia doveva essere "quantizzata". In pratica i vari sistemi fisici possono scambiare energia soltanto in quantità ben definite: a pacchetti o "quanti". Il quanto elementare di energia è legato ad una costante universale la costante h, che oggi chiamiamo costante di Planck e che vale 6.62618´10-34 J s. Planck fu il primo ad introdurla per spiegare lo spettro di corpo nero. Solo in un secondo momento, a partire dagli anni 20 del XX secolo si cominciò a sviluppare una teoria organica che portò alla moderna meccanica quantistica. Non è lo scopo di questa discussione parlare della meccanica quantistica ma non si può non sottolineare che la nuova fisica dà una visione probabilistica della realtà microscopica in contrasto con la visione deterministica del mondo macroscopico dato dalla fisica classica. Gli stessi concetti di realtà fisica e di misura delle grandezze fisiche hanno subito un mutamento radicale. Quando si studia o si osserva il mondo microscopico non possono essere utilizzati gli stessi concetti e metodi di descrizione che si usano per lo studio del mondo macroscopico. La situazione all’inizio del XX secolo: cinque problemi per la fisica classica.
Questi problemi furono affrontati e trovarono una spiegazione in termini della così detta "vecchia teoria quantistica". Lo spettro di corpo nero fu uno dei punti di partenza per lo sviluppo della nuova fisica. Fu Planck (1858-1947) che per primo sviluppò un modello soddisfacente per la sua comprensione. Einstein (1879-1955) sviluppò le teorie per l’effetto fotoelettrico e il calore specifico dei solidi. I modelli atomici che permettevano di dedurre anche la natura delle righe spettrali furono dovuti al lavoro di vari fisici in particolare al lavoro di Niels Bohr (1885-1962). che prese come base il lavoro di Ernest Rutherford (1871-1937). In questa discussione ci occuperemo un po’ più approfonditamente dell’effetto fotoelettrico. Tuttavia conviene partire da qualche considerazione sullo spettro di corpo nero per vedere perché sia necessario introdurre una quantizzazione dell’energia per interpretare ciò che gli esperimenti mostrano. Il corpo nero è un modello ideale tuttavia può essere sperimentalmente simulato da una cavità in equilibrio termodinamico (sostanzialmente che abbia una temperatura omogenea). E’ sperimentalmente noto che un corpo "caldo" emette (e assorbe) radiazione secondo uno spettro continuo. Più è alta la temperatura del corpo maggiore risulta l’intensità della radiazione emessa. Non solo, se la temperatura è sufficientemente alta la radiazione diventa visibile all’occhio (filamento di una lampadina). Se la temperatura del corpo è abbastanza elevata anche la forma dello spettro si avvicina a quella che si ottiene da un piccolo foro praticato in una cavità a temperatura uniforme (uguale alla temperatura del corpo). Il corpo nero rappresenta pertanto il modello limite che emette e assorbe radiazione a tutte le energie secondo uno spettro continuo di forma ben determinata che dipende solo dalla sua temperatura. La cosa particolarmente interessante (che era stata anche osservata sperimentalmente) è che la forma dello spettro di corpo nero dipende solamente dalla temperatura e non dalla natura del materiale di cui è fatta la cavità. I fisici del XIX secolo erano dell’opinione che la forma e le varie caratteristiche dello spettro dovessero essere calcolabili, a partire da considerazioni termodinamiche, in base alle leggi dell’elettromagnetismo. Il problema che si trovarono ad affrontare è il seguente: calcolare il numero di modi in cui si può distribuire l’energia in una cavità. Se ci rifacciamo all’esempio unidimensionale di una corda vibrante tra due estremi (una corda da chitarra per intenderci), sappiamo che le lunghezze d’onda permesse sono determinate dalla lunghezza della corda. In particolare se indichiamo con L la lunghezza della corda il primo modo (modo fondamentale o prima armonica) avrà una lunghezza d’onda l1=2L., il secondo modo l2=L; in generale gli infiniti modi possibili saranno del genere ln=2L/n. Il caso tridimensionale è più complesso ma i ragionamenti da fare sono simili. La termodinamica stabilisce (principio di equipartizione dell’energia) che l’energia del corpo nero si deve distribuire equamente su tutti i possibili modi. Il principio di equipartizione stabilisce che ad ogni grado di libertà (ogni modo possibile) compete, all’equilibrio termodinamico, un’energia data da:
Dove k è la costante di Boltzman (k=1.381´10-23 JK-1) e T e la temperatura assoluta. Nel caso delle onde elettromagnetiche il fattore 1/2 non c’è a causa delle due possibili polarizzazioni. La fisica classica permette di calcolare il numero dn di modi compresi in ogni intervallo dl compreso tra una qualunque lunghezza d’onda l e l+dl. Lo spettro osservato sperimentalmente dovrebbe allora essere descritto dal grafico kTdn in funzione di l. Va notato che già nel caso di una corda vibrante il numero dn di modi cresce al diminuire di l, tale crescita è ancora maggiore nel caso tridimensionale. Il calcolo in tre dimensioni del numero dn di modi compresi tra l e l+dl fornisce.
Dove con V si è indicato il volume della cavità. Per ottenere la densità di energia per unità di volume della cavità compresa tra le lunghezze d’onda l e l+dl, basta dividere per V e moltiplicare per l’energia corrispondente kT.
Il risultato descrive bene lo spettro di corpo nero a grandi lunghezze d’onda ma diverge per valori piccoli di l. Tale comportamento ha preso il ben noto nome di "catastrofe ultravioletta". L’apporto fondamentale di Planck alla fisica fu nel comprendere che le energie possibili per i vari modi all’interno della cavità non hanno una distribuzione continua come previsto dalla fisica classica ma possono assumere solo valori discreti. In particolare l’energia di un’onda stazionaria di lunghezza d’onda fondamentale l (frequenza n = c/l) può assumere solo dei valori discreti multipli di una quantità elementare data da:
Dove h è la costante universale di Planck. Le energie possibili sono pertanto date da e = nhn. Si noti che per grandi lunghezze d’onda il quanto di energia e diventa molto piccolo (limite classico: i valori possibili per l’energia diventano "quasi" continui). Sotto questa ipotesi l’energia media per modo viene a differire sostanzialmente da quella prevista classicamente (kT) in quanto viene a diminuire al decrescere della lunghezza d’onda.
Con questo risultato moltiplicato per il numero di modi precedentemente calcolato si ottiene un modello teorico che è in ottimo accordo con i dati sperimentali. Da esso si ricavano come casi limite anche le espressioni trovate da Rayleigh-Jeans (per le grandi lunghezze d’onda: limite classico), la legge di Wien, per lo spostamento del massimo dello spettro di corpo nero, e la legge di Stefan-Boltzman che fornisce l’energia emessa da un corpo nero ad una data temperatura. Effetto fotoelettrico. L’esperienza mostra che sotto certe condizioni un metallo colpito da un fascio di luce emette elettroni. Cosa è spiegabile dalla fisica classica, almeno approssimativamente.
Ma ci sono altre osservazioni non interpretabili in termini della fisica classica. Inoltre esiste fotoemissione di elettroni anche per i gas e la corrente di elettroni emessi dipende dall’angolo di incidenza della radiazione incidente e dalla sua polarizzazione. Quest’ultimo fatto non è interpretabile nella "vecchia teoria quantistica". Interpretazione di Einstein. In un fascio di luce monocromatica l'energia si propaga in quanti di luce hn dove n è la frequenza dell'onda e h è una costante universale (già introdotta da Planck per interpretare lo spettro di radiazione del corpo nero).
dove
L'elettrone del metallo può"assorbire" il quanto di luce. Se l'energia con cui è legato quest'elettrone è W0 e se hn ³ W0 l'elettrone può venire espulso dal metallo. L'energia cinetica dell'elettrone espulso sarà:
W0 è evidentemente una energia caratteristica di ogni materiale; essa prende il nome di potenziale di estrazione: W0 è il lavoro che bisogna fare per "strappare l'elettrone dalla sostanza". Questa relazione spiega la dipendenza lineare dell'energia cinetica dalla frequenza della luce incidente. Sfruttando la relazione ricavata da Einstein si può di misurare la costante e di Planck h. La misura fu effettuata da Millikan. Per la misura dell'effetto fotoelettrico Einstein e Millikan ricevettero il premio Nobel per la fisica nel 1921 e nel 1923 rispettivamente.. Esperimento
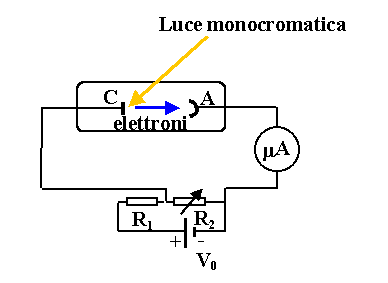
Quando il catodo emettitore viene colpito da luce di opportuna frequenza (lunghezza d’onda), vengono emessi elettroni. Se il potenziale dell'elettrodo (anodo) è zero (VA=0) una parte di questi elettroni possono raggiungere l'anodo ed il galvanometro indicherà passaggio di corrente elettrica (purché hn sia maggiore uguale di W0). Si può supporre , per la relazione di Einstein, che tutti gli elettroni abbiano la stessa energia cinetica (ciò è vero a meno di effetti termici).
Se il potenziale dell'anodo è maggiore di zero (VA>0) un maggior numero di elettroni saranno raccolti dall'elettrodo e la corrente crescerà al crescere del potenziale finché, per VA sufficientemente elevato, tutti gli elettroni emessi raggiungeranno l'elettrodo (condizione di saturazione). Se il potenziale dell'anodo è minore di zero (VA<0) gli elettroni vengono frenati dal potenziale negativo –VA. Per un certo valore del potenziale negativo applicato all’elettrodo la corrente di fotoelettroni si annulla; il valore di 0 per la corrente lo si ottiene quando:
In questa relazione e è la carica dell’elettrone (e=1.6x10-19Coulomb). Quindi se -eVA³Ecin nessun elettrone può raggiungere l’elettrodo. Pertanto si può scrivere la seguente relazione
Dove si è postoV0=-VA* e VA* rappresenta il valore del potenziale di anodo VA per il quale la corrente di fotoelettroni si annulla. Questa è una relazione lineare tra V0 e n. Registrando vari valori del potenziale dell'anodo V0, per cui la corrente si annulla, al variare della frequenza n dei fotoni incidenti, si può costruire una retta la cui pendenza è
e la cui intercetta è
W0/e per i metalli alcalini vale circa 1V e pertanto può essere misurata nel visibile (hn nel visibile vale circa 1 eVolt).
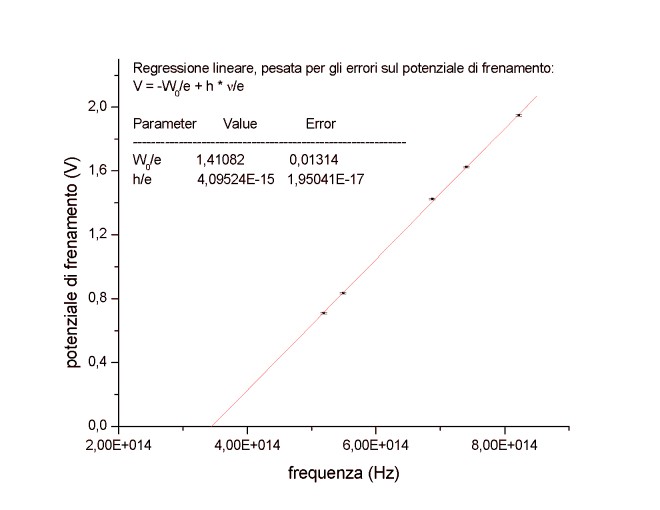
Con i dati raccolti, si ottiene il seguente grafico dal quale si ricava, con il metodo dei minimi quadrati pesati, la retta che interpola meglio i dati.
Utilizzando i valori ricavati con il metodo dei minimi quadrati, moltiplicando per il valore tabulato di e (1,602E-19 C), si ottiene tale valore, tenuto conto anche del fatto che l'errore sul potenziale di frenamento è sottostimato, è in buon accordo con quello tabulato: |